BFS is the simplest algorithm to find a node in a graph.
Given a graph G = (V, E) and a vertex s to search, breadth first search algorithm finds all the elements reachable element from s, along with finding the element it computes the distance of the each reachable vertices and creates a BFT with root as s. For any vertex u reachable from s, the path in the BFT from s to u corresponds to the Shortest path in G.
Breadth First Search expands frontier between discovered and undiscovered uniformly across the breadth. i.e. As part of this algorithm first all the node at height K is discovered before discovering any node at depth k+1… BFS works both for directed and undirected graphs.
Algorithm
In this algo to keep track the progress, three colors will be used.- White: Initial stage of all the vertices.
- Black: Vertex has been marked black if it does not have any white vertices next to it.
- Grey: A vertex is marked grey if it has adjacent vertices of any color.
Graphic display of the algorithm
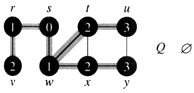
G = (V,E)V = {r, s, t , u, v, w, x, y};
E = {r-s, s-w, r-v, w-t, w-x, t-u, t-x, u-y, x-y}
First step: All the vertices are marked as white except source vertices. We will mark source vertex as Grey and add it into the queue.

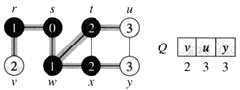
Second Step: It will retrieve one element from the queue and mark the fetched element as Black and will push its adjacent elements to the queue marking them as grey.
 \
\here as you can see, s has been deleted from the queue and now marked as black. Adjacent element of s i.e. w and r are added to the queue.
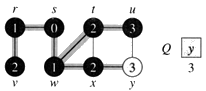
Next: Second step will be followed till queue do not have any more elements. At each vertex level the distance of the vertex is also stored.



Pseudo Code
Step 1: Assign white color to all the vertices, infinite for each vertex and to make it a tree it is necessary to have parent information, assign parent vertex as null to all vertices.Step 2: Add source to the queue. Assign distance 0. Change the color of the source as grey.
Step 3: Retrieve first element from the queue. Mark the retrieved element as black.
- Find all the adjacent white vertices of the retrieve vertex.
- Mark them grey.
- Set the distance of the adjacent vertices to one more than the distance of existing vertex.
- Add them to queue.
Pseudo Code in programmatically
1: BFS(G,s) 2: 3: for each vertex u in V[G] - {s}
4: do color[u] = white
5: dist[u] = inf 6: parent[u] = nil 7: 8: color[s] = G 9: dist[s] = 0 10: parent[s] = nil 11: Q.add(s) 12: 13: while( Q is empty){
14: 15: do u = delete(Q){
16: for each v in adj[u] {
17: 18: do if color[v] = w {
19: 20: color[v] = G 21: parent[v] = u 22: dist[v] = dist[u] + 1 23: Q.add(v) 24: 25: } 26: 27: } 28: } 29: 30: color[u] = B 31: 32: }Java Code
There is the Java code for the pseudo code mentioned above. I do not think there is need to explain this here.1: import java.util.HashMap;
2: import java.util.List;
3: import java.util.Map;
4: import java.util.Queue;
5: import java.util.Set;
6: import java.util.concurrent.SynchronousQueue;
7: 8: 9: public class BFS {
10: 11: Map<String, List<String>> graph; 12: BFTNode sourceNode;13: Map<String, BFTNode> tree = new HashMap<String, BFTNode>();
14: 15: BFS(Map<String, List<String>> g, String source){ 16: graph = g;17: sourceNode = new BFTNode(source);
18: } 19: 20: void createBFTNodes(){
21: Set<String> vertices = graph.keySet();22: for(String vertex : vertices){
23: tree.put(vertex, new BFTNode(vertex));
24: 25: } 26: } 27: 28: void algorithm(){
29: 30: createBFTNodes(); 31: sourceNode.setColor(1); 32: 33: Queue<BFTNode> Q = new SynchronousQueue<BFTNode>();
34: Q.add(sourceNode); 35: 36: do{
37: 38: BFTNode node = Q.remove(); 39: List<String> adjacentVertices = graph.get(node.getVertex()); 40: 41: for(String adjacentVertex : adjacentVertices){
42: 43: BFTNode temp = new BFTNode(adjacentVertex);
44: temp.setColor(1); 45: temp.setDist(node.getDist() + 1); 46: temp.setParent(node); 47: Q.add(temp); 48: tree.put(adjacentVertex, temp); 49: 50: } 51: 52: node.setColor(2); 53: tree.put(node.getVertex(), node); 54: 55: }while(Q.size() > 0);
56: 57: } 58: 59: } 60: 61: //This class has getter/Setter method for all the property that a tree node require.
62: class BFTNode{
63: 64: private int dist = 0;
65: private int color = 0;
66: private BFTNode parent = null;
67: private String vertex = "";
68: 69: public BFTNode(String name) {
70: vertex = name; 71: } 72: 73: public String getVertex() {
74: return vertex;
75: } 76: 77: public int getDist() {
78: return dist;
79: } 80: 81: public void setDist(int dist) {
82: this.dist = dist;
83: } 84: 85: public int getColor() {
86: return color;
87: } 88: 89: public void setColor(int color) {
90: this.color = color;
91: } 92: 93: public BFTNode getParent() {
94: return parent;
95: } 96: 97: public void setParent(BFTNode parent) {
98: this.parent = parent;
99: } 100: 101: public boolean equals(Object anotherObject){
102: if (anotherObject instanceof BFTNode){
103: return vertex.equals(((BFTNode)anotherObject).vertex);
104: }105: return false;
106: } 107: 108: public int hashCode(){
109: return vertex.hashCode();
110: } 111: 112: public String toString(){
113: if(parent != null)
114: return ("Vertex:" + vertex + " Color:" + color + " Dist:" + dist + " Parent:" + parent.vertex);
115: else
116: return ("Vertex:" + vertex + " Color:" + color + " Dist:" + dist + " Parent: Null");
117: } 118: }Analysis
It is always mandatory to know how is the performance and resource utilization of the algorithm.Time taken for the algorithm is O(V+E). This algorithm has linear time complexity which particularly depends upon the sum of the vertices and edges of the graph.
Other Algos implementing this algorithm internally
- Dijkstra’s Single Source Shortest Path Algorithm
- Prim’s Minimum Spanning tree Algorithm
